09III/09IV (093/094) Nuclear Submarine Thread
- Thread starter SinoSoldier
- Start date
I know the difference very well.
Quickie
Colonel
If I can just add to the discussion.
You're right that cavitation occurs both at lower and higher pressure. I think that the higher pressure at the greater depth allows the propeller to go at a higher speed than that at the lower pressure of a lesser depth before cavitation would even occur.
Meaning that a submarine would simply go to a deeper depth to increase its speed to the limit that is just before the point when cavitation would start to occur.
Last edited:
Hendrik_2000
Lieutenant General
It doesn't simply because the higher the propeller speed the more low pressure(vacuum) it generate and vapor will form. It function of propeller speed only.This is Bernoulli law at the interface of propeller and water. As bubble grow it will separate But the static pressure around it higher so it will pop
Static pressure=(Rho)gH where Rho is specific weight(constant); g is constant; H is the water column height above sub. So the deeper the sub dive the higher the number is. The bubble will pop earlier
To avoid cavitation you just have to slow the speed and make the propeller larger, make every rotation count That mean high efficiency propeller
Last edited:
Having the MESMA on the Short Fin Barra. makes sense since it is a derivative of the nuclear powered Barracuda. All the doubts with regards to having enough power from batteries to run the pump jets answered. I realise this is out of topic but i want to add my two cents on the question of whether Australia may opt to go nuclear on the last few of the planned 12 boats,would never happen because of Australians fierce resistance to anything to do with nuclear power.Monsieur hehemake sense he use this AIP but i am not sure also planned for Scorpene but right now no Scorpene in sevice equiped for soon/later 6 Indians don' t have, Brazil i don' t think.
Pakistanese Agosta 90B have.
Quickie
Colonel
The bubbles will not be easier to pop at higher pressure of greater depth anymore than at lower pressure of lesser depth.
The reason is because cavitation at greater depth happens at higher pressure which in turn form bubbles with the same equal higher pressure within it. The higher pressure within the bubbles balances the higher pressure at the greater depth such that the bubbles wouldn't be anymore easier to pop than in the case when it's formed at a lower pressure condition.
Hendrik_2000
Lieutenant General
Watch again the experiment imagine the Beaker as the CV(control volume at the interface of propeller blade and water) and the atmospheric outside the glass as static head
As soon as he reduce the pressure in the beaker water vapor is created irrespective of the pressure outside the beaker which is atmospheric
Vapor pressure is thermodynamic property depend only on temp and press. Since there is no heat input here .It depend only on pressure . The experiment show if you reduce the pressure low enough it will bubble . The vacuum is created due to rotation of the propeller.
This is not the same of pressure cooker. what you describe is pressure cooker process. It is the opposite of pressure cooker process
Last edited:
Quickie
Colonel
Even if the air in the flask is totally removed, the bubbles are still under the pressure of the column of water in the flask. It doesn't really mean the pressure in it suddenly become irrelevant in the absence of atmospheric pressure.
A 10m meter tall flask filled with water would have the same atmospheric pressure at sea level, even with the air totally removed from the flask, and you would need to heat the water to 100 degree C to cause it to boil. The same with the cavitation process . At higher pressure you would need higher input energy to initiate the cavitation process by way of increasing the speed of the propeller.
I believe Quickie is correct that the onset speed of cavitation is higher the deeper you go. I have read Tom Clancy's "SSN" and non-fiction "Submarine", in which he goes on to explain this phenomenon and how it applied to the Los Angeles class. Not a technical source, but I doubt Clancy made up the physics. His earlier work is imho rather well researched.
Hendrik_2000
Lieutenant General
I think you confuse the thermodynamic control volume with the real world volume
Thermodynamic control volume is fictitious boundary condition where the conservation of energy process occur.
The bernoulli process occur only in the thermodynamic control volume. So rotating the propeller speed inside this CV will increase cavitation. so my analogy of beaker is correct
System and Control Volume
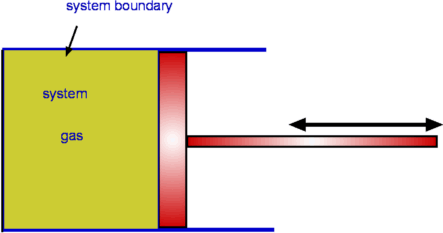
Figure 3.12 : Piston cylinder arrangement
Terms system and control volume are very familiar to the one who has studied thermodynamics. The word system refers to a fixed mass with a boundary. However, with time the boundary of the system may change, but the mass remains the same. The usual example given is that of a piston-cylinder arrangement as shown in Fig.3.12. Consider a gas filled in the cylinder which is closed by a piston at the right hand end. Let us define gas as our system. If the piston is now operated by pushing or pulling it the gas compresses or expands. The boundary of our system moves. But the mass does not move out of the boundary since by definition system is a fixed mass. The definition does not prevent work or energy crossing the boundary.
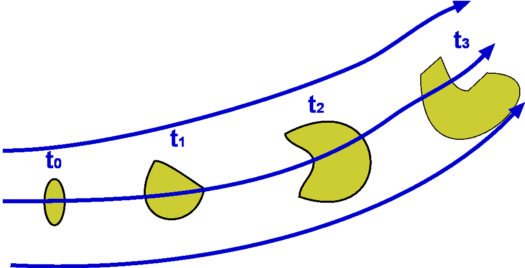
Figure 3.13 : System Approach
It is easy to analyse the system in the example of piston-cylinder arrangement that we have considered before. But the question is - Are all systems as simple as this? The answer is obviously a "no". In fluid dynamics we consider systems which are far more complicated. Take the flow about an aeroplane for example. If we define a system in such a flow and try to analyse it we find that it undergoes many changes as ilustrated in Fig. 3.13. The boundary changes rapidly and undergoes unmanageable distortions. The system approach is almost ruled out. The other examples are flow through turbomachinery, flow in hydraulic systems and many such.
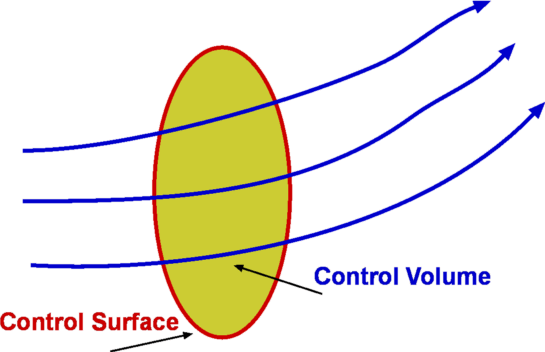
The other method we have is the Control Volume approach. Here we do not focus our attention on a fixed mass of fluid. Instead we establish a "window" for observation in the flow. This is what we call the control volume shown in Fig. 3.14. As against the system, a control volume has a fixed boundary. Mass, momentum and energy are allowed to cross the boundary. We perform a balance of mass, momentum and energy that flow across the boundary and deduce the changes that could take place to properties of flow within the control volume. The shape of the control volume does not change normally. It is easy to visualise that this is a convenient approach. in fact, it is the one that is commonly used in fluid dynamics.
Figure 3.14 : Control Volume
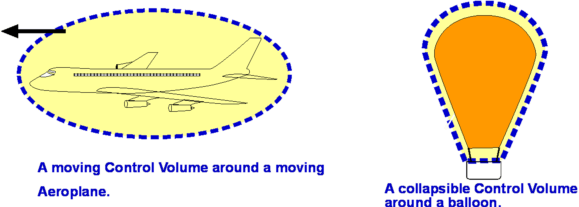
We will consider a fixed control volume most of the time. But it is possible to have control volumes that change their boundary, those that deform etc. Obviously, these lead to more complicated equations. Examples of such control volumes are given in Fig.3.15.
Figure 3.15 : Moving and Collapsible Control Volumes
The boundary of the control volume is referred to as control surface.
From the above discussion it is clear that the system and control volume approaches are akin to Lagrangian and Euler approaches.
Last edited: