Chauvinistic?
News on China's scientific and technological development.
- Thread starter Quickie
- Start date
Yup we invented that word as we called outsiders as barbarians not Mexican Hombre.
Robust spectral reconstruction algorithm enables quantum dot spectrometers with subnanometer spectral accuracy
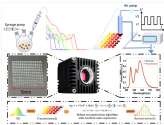
Since the concept of computational spectroscopy was introduced, numerous computational spectrometers have emerged. While most of the work focuses on materials, optical structures, and devices, little attention is paid to the reconstruction algorithm, thus resulting in a common issue: the effectiveness of spectral reconstruction is limited under high-level noise originating from the data acquisition process. Here, we fabricate a computational spectrometer based on a quantum dot (QD) filter array and propose what we believe is a novel algorithm, TKVA (algorithm with Tikhonov and total variation regularization, and the alternating direction method of multipliers), to suppress the impact of noise on spectral recovery. Surprisingly, the new TKVA algorithm gives rise to another advantage, i.e., the spectral accuracy can be enhanced through interpolation of the precalibration data, providing a convenient solution for performance improvement. In addition, the accuracy of spectral recovery is also enhanced via the interpolation, highlighting its superiority in spectral reconstruction. As a result, the QD spectrometer using the TKVA algorithm shows supreme spectral recovery accuracy compared to the traditional algorithms for complex and broad spectra, a spectral accuracy as low as 0.1 nm, and a spectral resolution of 2 nm in the range of 400 to 800 nm. The new reconstruction algorithm can be applied in various computational spectrometers, facilitating the development of this kind of equipment.
US politicians: “Our Chinese will beat their Chinese”.
Xi: “Your Chinese are becoming our Chinese. BTW I’ll trade you some human-powered dishwashers if you need to meet ethnicity quota.”